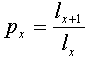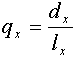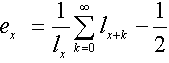Anwendung der Sterbetafel in der Lebensversicherung
Aus mathematischer Sicht ist die Lebensversicherung nur ein Anwendungsgebiet der Zinseszins- und Rentenrechnung. Dabei unterscheidet man u. a. eine Versicherung auf den Todes- und Erlebnisfall, eine Invaliden- und Altersversicherung oder eine Sparrentenversicherung. Bei jeder dieser Versicherungen gehen die Versicherungsanstalt und der Versicherungsnehmer einen Vertrag ein. Zwischen den Zahlungen des Versicherungsnehmers und den Leistungen der Versicherungsanstalt, die sich u. a. nach der Art der Versicherung richten, muss Gleichwertigkeit bzw. Äquivalenz bestehen, wenn der Versicherungsvertrag für keinen der Beteiligten zu einem Verlust führen soll. Natürlich gilt die Gleichwertigkeit der Aufwendungen nicht für den einzelnen Versicherten, denn dann wäre die Versicherung überflüssig, sondern nur für die Menge aller Versicherten.
Zudem relativiert sich die Gleichwertigkeit der Aufwendungen durch Kapitalmarktrelationen (z. B. durch eine Hochzinsphase) und den Grad der "geographischen" (Ab?)Geschlossenheit der betrachteten Systeme. Letzteres zeigt sich bei der einfachen praktischen Frage nach der Sterbetafel, die für einen Griechen angewendet werden sollte, der z. B. seit dem 10. Lebensjahr in Frankreich wohnt, aber auf dem offenen EU-Markt eine deutsche Lebensversicherung vereinbaren möchte. Immerhin kämen in diesem Fall drei unterschiedliche Sterbetafeln zur Anwendung. In der Praxis unterscheiden die großen deutschen Versicherungsanstalten bei Lebensversicherungen aber nur Kunden mit Wohnsitz in Deutschland von Kunden, denen eine Auslandsversicherung angeboten wird (Wohnortprinzip).
Bei der mathematischen Formulierung des Äquivalenzprinzips spielen neben der Zinssatz- und Rentenrechnung u. a. demographische (bevölkerungsstatistische ) Annahmen eine Rolle.
Das wichtigste demographische Hilfsmittel der Lebensversicherungsanstalten ist dabei die Sterbetafel. Sie beruht teils auf Volkszählungen und Fortschreibungen, teils auf den langjährigen Erfahrungen der Versicherungsanstalten. Sie gehen von einer bestimmten großen (im übrigen willkürlich gewählten!) Anzahl kn gleichaltriger, nämlich n-jähriger Personen aus und geben an, wie viele von diesen das x-te (Lebens-)Jahr erreichen. Diese Anzahl von Personen wird mit lx bezeichnet und wird Anzahl der Lebenden des Alters x genannt. Außerdem sind in den Tafeln folgende Beziehungen enthalten: