Die globale Bevölkerungsentwicklung beschränkt sich in absehbarer Zeit auf die natürliche Bevölkerungsbewegung. Langfristig war sie stets durch Zunahme gekennzeichnet, so dass dafür fast synonym der Ausdruck Bevölkerungswachstum verwendet wird. Wachstum wird in absoluten Zahlen (Differenz zweier Bevölkerungsstände) oder relativ als Wachstumsrate (jährlicher absoluter Zuwachs je 100 bzw. je 1 000 Einwohner der Ausgangsbevölkerung) angegeben. In ausgewählten Gebieten und Perioden kann sich die Bevölkerungszahl verringern. In diesem Fall wird von einer rückläufigen Bevölkerungsentwicklung oder, in Anlehnung an die Ökonomie, von Schrumpfung bzw. von einem negativen Wachstum gesprochen.
In den Jahrtausenden der anthropogenen Evolution und den Jahrhunderten der sozialen Entwicklung bis hinein ins Mittelalter nahm die Bevölkerung der Erde nur langsam zu; zuweilen stagnierte sie und oft verringerte sie sich sogar dramatisch. Dieses Wachstum war noch stark von der Naturabhängigkeit der damaligen Gesellschaften in ihrer Bindung an das jeweilige Entwicklungsniveau der Produktivkräfte, also die Gesamtheit der individuellen und sozialen Produktionsfaktoren, abhängig. Damit ähnelt das Wachstum stark dem rein biologischer Systeme, die in der Biologie durch Modelle der Populationsdynamik beschrieben werden. Auch die frühen Demographen und Bevölkerungsgeographen verwendeten solche Modelle. Am bekanntesten ist die Orientierung von MALTHUS auf das exponentielle Wachstum der Bevölkerung. Die Tragfähigkeitsansätze, bei denen Wachstumsgrenzen und die maximal mögliche Bevölkerungszahl als Kapazität des existentiellen Rahmens definiert werden, bedienen sich ebenfalls derartiger Modelle
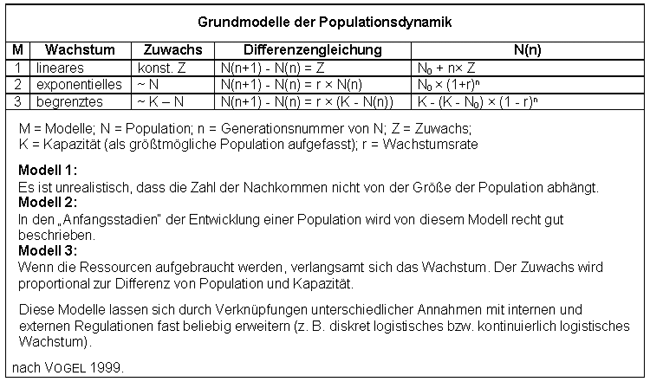
Die demographische Grundgleichung ist also die allgemeinste Form aller Wachstumsmodelle (Neue Population = Alte Population + Zuwachs) mit dem Wachstum als Differenz zweier Populationsgrößen zu verschiedenen Zeiten. Dieses Differenzenkalkül vernachlässigt nicht nur die Strukturen der Population und ihre Existenzbedingungen, sondern auch die verstrichene Zeit. Wird letztere mit einbezogen, gelangt man rasch zu Differentialgleichungen, die u. a. schon von CZUBER (1923) zur Bestimmung und Beschreibung außerordentlich komplexer Bevölkerungsstrukturen und -prozesse entwickelt wurden. Interessant war sein Versuch, mit Algorithmen und Verfahren der Differential- und Infinitesimalrechnung eine Wachstumsrate für die Weltbevölkerung aus der damals bekannten Zeitreihe der Bevölkerungszahlen abzuleiten und auf ihre inhaltliche Aussage zu überprüfen. CZUBERs Aussagen (vgl. Übersicht CZUBER) werden hier etwas ausführlicher als andere dargestellt, da sie in mehrfacher Hinsicht ein bemerkenswertes Zeugnis darstellen: